Appendix B — Trivial Endpoints

B.1 Background

A “trivial” endpoint is a fixed point or a global optimum that consists of a singleton theory (e.g. \(T=\lbrace s_{1}\rbrace\)) and a singleton commitment (e.g. \(C = \lbrace s_{1}\rbrace\)).

Such outcomes are not bad per se, but they may be indicative of the model exploiting shortcomings in the underlying measures. In particular, “trivial” endpoints may be a consequence of the original model’s shortcoming concerning the measure of systematicity, which does not discriminate between singleton theories on the basis of the scope of theories. Note that the same shortcoming also applies to the model variants explored in this report.

B.2 Results

Note

The results of this chapter can be reproduced with the Jupyter notebook located here.

B.2.1 Overall Results

Model	Relative share of trivial global optima	Number of trivial global optima	Number of global optima
QuadraticGlobalRE	0.009	6625	714584
LinearGlobalRE	0.081	56635	700830
QuadraticLocalRE	0.009	6625	709289
LinearLocalRE	0.07	50256	721096

Table B.1: Relative share of trivial global optima

Model	Relative share of trivial fixed points	Number of trivial fixed points	Number of fixed points
QuadraticGlobalRE	0.008	3698	458147
LinearGlobalRE	0.08	25111	312783
QuadraticLocalRE	0.009	5189	588236
LinearLocalRE	0.063	14443	228122

Table B.2: Relative share of trivial fixed points (result perspective)

Model	Relative share of trivial fixed points	Number of trivial fixed points	Number of fixed points
QuadraticGlobalRE	0.007	3700	528616
LinearGlobalRE	0.08	25111	313002
QuadraticLocalRE	0.006	11652	1991852
LinearLocalRE	0.323	421058	1303077

Table B.3: Relative share of trivial fixed points (process perspective)

Observations

• Overall, the relative share of trivial gobal optima (Table B.1) and fixed points (result perspective Table B.2) is very low for quadratic model variants
• Linear model variants exhibit substantially more trivial global optima, but the relative shares are still low.
• LinearLocalRE exhibits a substantial share of trivial fixed points in the process perspective (Table B.3), but not for the result perspectve (Table B.2). This indicates that relatively many branches lead to trivial fixed points.

B.2.2 Results Grouped by Sentence Pool Size

Figure B.1: Relative share of trivial global optima grouped by model variant and sentence pool size

Figure B.2: Relative share of trivial fixed points (result perspective) grouped by model variant and sentence pool size

Figure B.3: Relative share of trivial fixed points (process perspective) grouped by model variant and sentence pool size

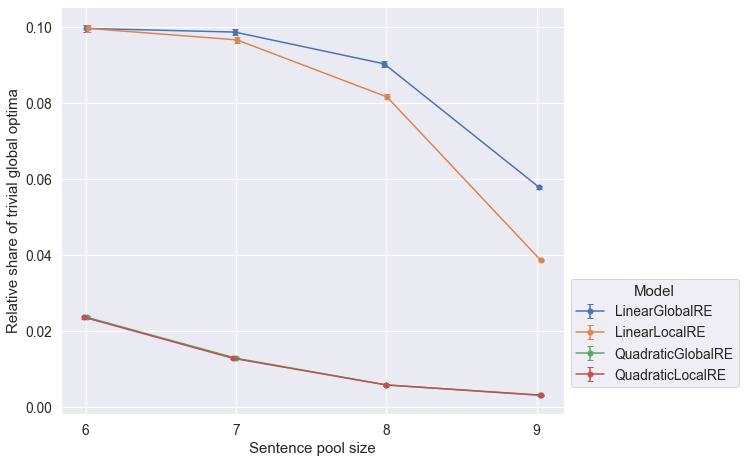
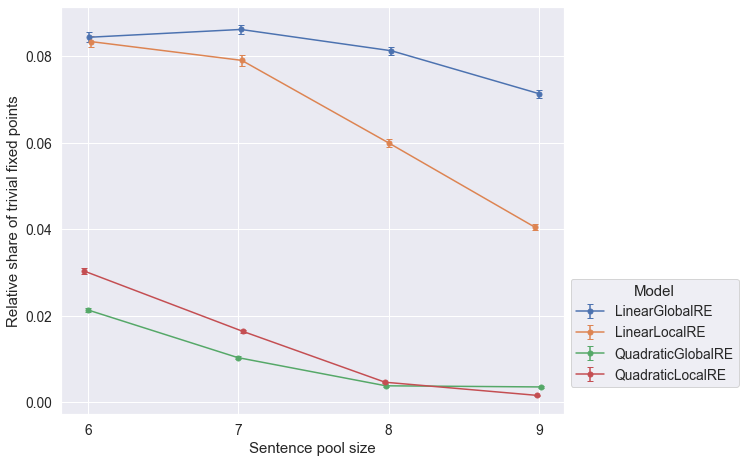
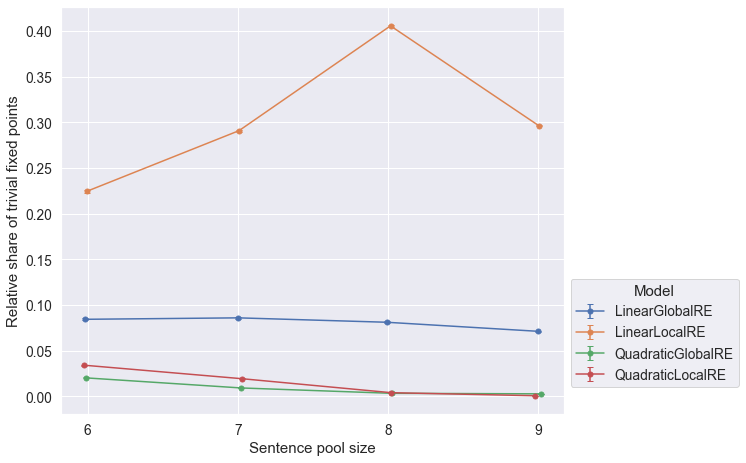
Observations

• The relative shares of trivial global optima or fixed points tend to decrease with increasing sentence pool sizes.
• A notable exception to this trend is LinearLocalRE in the process perspective (Figure B.3)

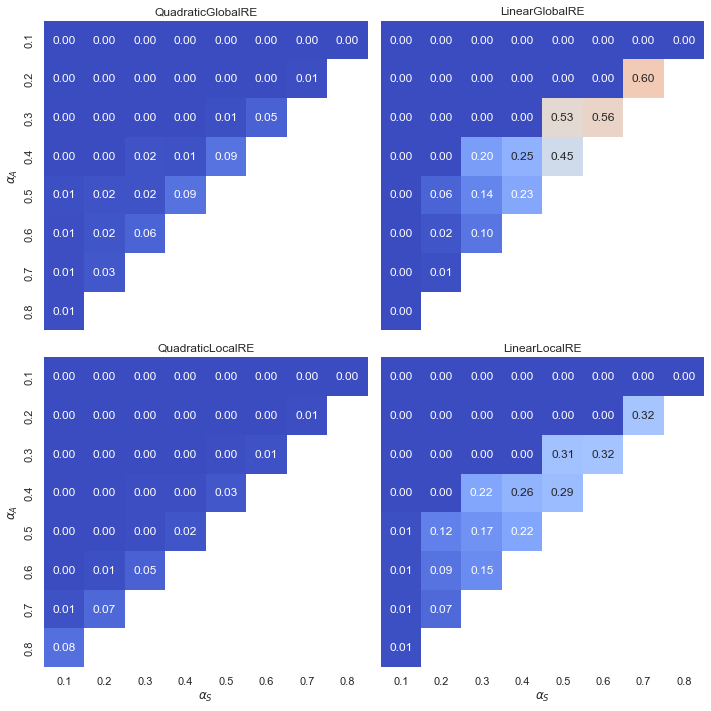
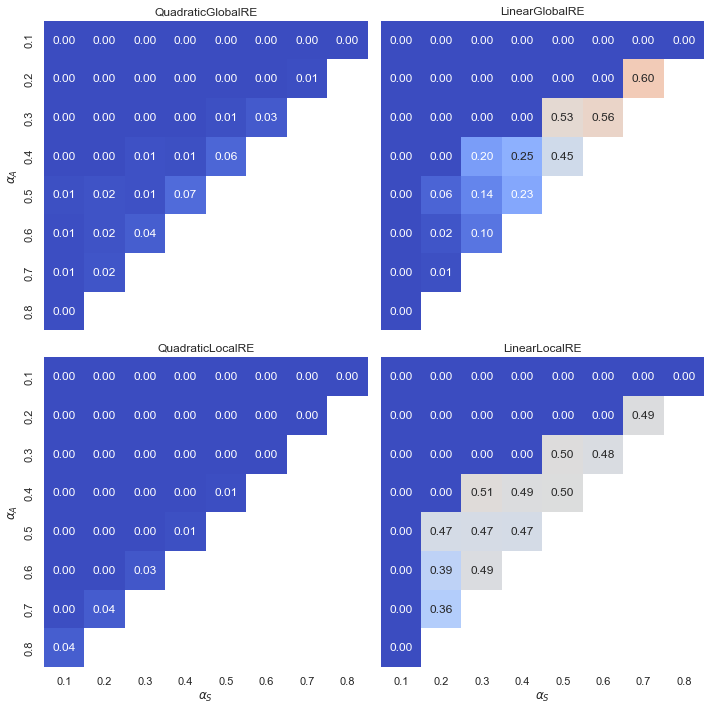
B.2.3 Results Grouped by Configuration of Weights

Figure B.4: Relative share of trivial global optima grouped by model variant and weight configuration

Figure B.5: Relative share of trivial fixed points (result perspective) grouped by model variant and weight configuration

Figure B.6: Relative share of trivial fixed points (process perspective) grouped by model variant and weight configuration

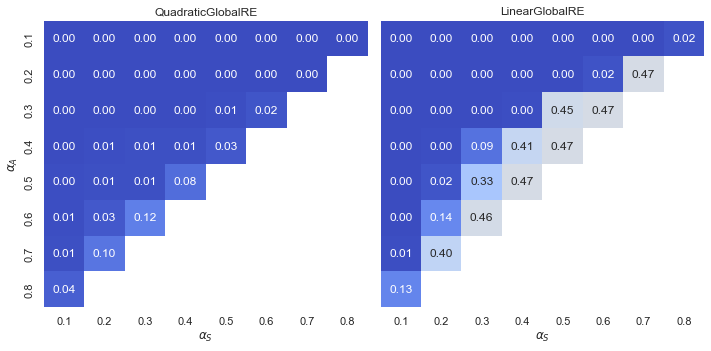
Observations

• In quadratic model variants, the configuration of weights have a small impact on the relative shares of trivial endpoints.
• Linear model variants tend to produce higher relative shares of trivial endpoints for low values of \(\alpha_{F}\) and high values of \(\alpha_{S}\).